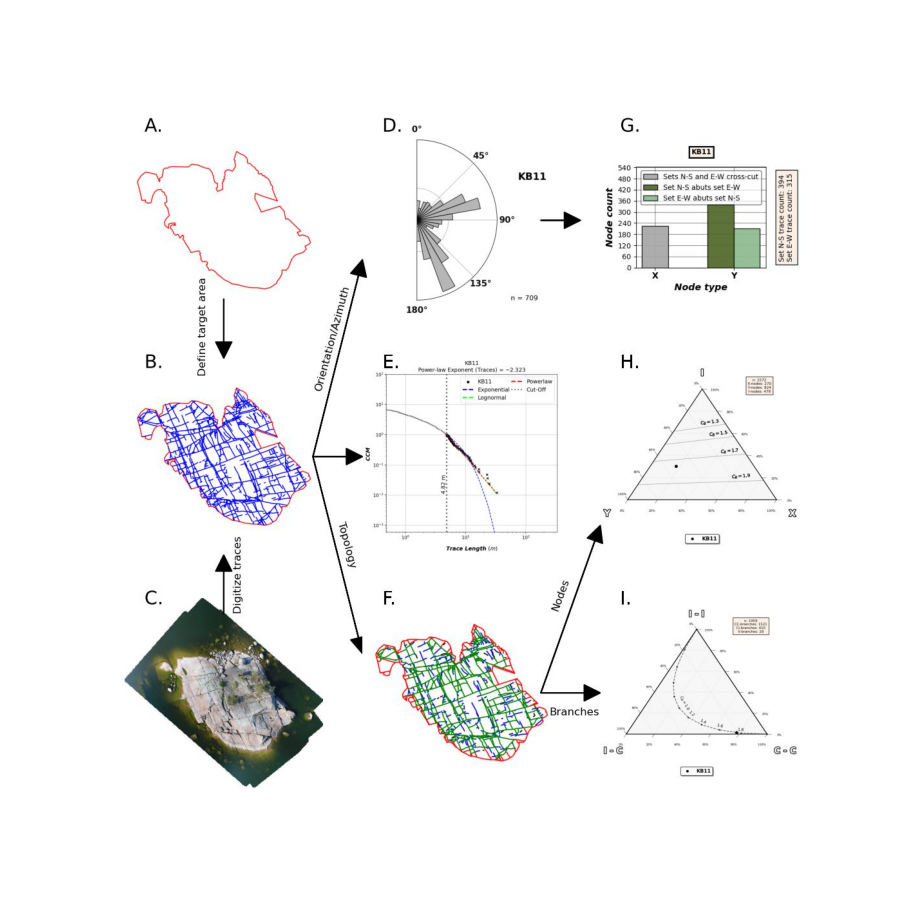
Workflow visualisation of fractopo

See examples/fractopo_workflow_visualisation.py for the code.

({'E-W': 1044, 'N-S': 1026}, {'E-W': 315, 'N-S': 394})
(('N-S', 'E-W'), ((135, 45), (45, 135)))
{'trace Kolmogorov-Smirnov critical distance value': np.float64(0.14838816536047483),
 'trace exponential Kolmogorov-Smirnov distance D': np.float64(0.16892974112367803),
 'trace exponential lambda': np.float64(0.28990030921409604),
 'trace exponential loglikelihood': np.float64(-188.01500959555236),
 'trace lengths cut off proportion': np.float64(0.8815232722143864),
 'trace lognormal Kolmogorov-Smirnov distance D': np.float64(0.05684340157325507),
 'trace lognormal loglikelihood': np.float64(-181.35887551595403),
 'trace lognormal mu': np.float64(-24.715475925652207),
 'trace lognormal sigma': np.float64(3.4173856212586093),
 'trace lognormal vs. exponential R': np.float64(1.8403353765911368),
 'trace lognormal vs. exponential p': np.float64(0.06571901465515168),
 'trace power_law Kolmogorov-Smirnov distance D': np.float64(0.05338771615349713),
 'trace power_law alpha': np.float64(3.3235301635943837),
 'trace power_law cut-off': np.float64(4.815579557192599),
 'trace power_law exponent': np.float64(-2.3235301635943837),
 'trace power_law sigma': np.float64(0.25351792509962834),
 'trace power_law vs. exponential R': np.float64(1.7925884033808193),
 'trace power_law vs. exponential p': np.float64(0.0730387620558565),
 'trace power_law vs. lognormal R': np.float64(-0.09952067980457371),
 'trace power_law vs. lognormal p': np.float64(0.9207248692966787),
 'trace power_law vs. truncated_power_law R': np.float64(-0.39489151701014713),
 'trace power_law vs. truncated_power_law p': np.float64(0.655109563188556),
 'trace truncated_power_law Kolmogorov-Smirnov distance D': np.float64(0.06244158664610938),
 'trace truncated_power_law alpha': np.float64(3.1019932183797074),
 'trace truncated_power_law exponent': np.float64(-2.1019932183797074),
 'trace truncated_power_law lambda': np.float64(0.0169250701495417),
 'trace truncated_power_law loglikelihood': np.float64(-181.26870278046098)}
{'branch Kolmogorov-Smirnov critical distance value': np.float64(0.13209487728058794),
 'branch exponential Kolmogorov-Smirnov distance D': np.float64(0.058587502831379146),
 'branch exponential lambda': np.float64(1.312910825728923),
 'branch exponential loglikelihood': np.float64(-77.14234665862854),
 'branch lengths cut off proportion': np.float64(0.9487922705314009),
 'branch lognormal Kolmogorov-Smirnov distance D': np.float64(0.058192286328960674),
 'branch lognormal loglikelihood': np.float64(-77.31473693985473),
 'branch lognormal mu': np.float64(0.14893325862157306),
 'branch lognormal sigma': np.float64(0.5382505634183521),
 'branch lognormal vs. exponential R': np.float64(-0.3966894758839369),
 'branch lognormal vs. exponential p': np.float64(0.6915964618282773),
 'branch power_law Kolmogorov-Smirnov distance D': np.float64(0.05406513067687313),
 'branch power_law alpha': np.float64(5.109727683188838),
 'branch power_law cut-off': np.float64(2.4825527158400007),
 'branch power_law exponent': np.float64(-4.109727683188838),
 'branch power_law sigma': np.float64(0.3991720396819592),
 'branch power_law vs. exponential R': np.float64(-0.8370547306274025),
 'branch power_law vs. exponential p': np.float64(0.4025618046682585),
 'branch power_law vs. lognormal R': np.float64(-1.016822479615626),
 'branch power_law vs. lognormal p': np.float64(0.30923788618620074),
 'branch power_law vs. truncated_power_law R': np.float64(-1.2015352804556587),
 'branch power_law vs. truncated_power_law p': np.float64(0.10275119176828862),
 'branch truncated_power_law Kolmogorov-Smirnov distance D': np.float64(0.05738796319405115),
 'branch truncated_power_law alpha': np.float64(1.3430016659542363),
 'branch truncated_power_law exponent': np.float64(-0.3430016659542363),
 'branch truncated_power_law lambda': np.float64(0.9602580179354512),
 'branch truncated_power_law loglikelihood': np.float64(-77.02994823190853)}
('N-S', 'E-W')
((135, 45), (45, 135))
(('N-S', 'E-W'), ((135, 45), (45, 135)))
   name        sets    x    y y-reverse error-count
0  KB11  (N-S, E-W)  224  339       210           0
/nix/store/7cla11phfawchn96chhcyr9b135h14j4-python3.13-python-ternary-1.0.8/lib/python3.13/site-packages/ternary/plotting.py:148: UserWarning: No data for colormapping provided via 'c'. Parameters 'vmin', 'vmax' will be ignored
  ax.scatter(xs, ys, vmin=vmin, vmax=vmax, cmap=colormap, **kwargs)
{'node_counts': {'E': 114, 'I': 476, 'X': 268, 'Y': 826}}
{'branch_counts': {'C - C': 1521,
                   'C - E': 100,
                   'C - I': 408,
                   'E - E': 1,
                   'I - E': 12,
                   'I - I': 28}}
Saving workflow plot to /build/tmpl7hm1t3s/fractopo_workflow_visualisation.jpg

from pathlib import Path
from tempfile import TemporaryDirectory

import fractopo_workflow_visualisation
import matplotlib.pyplot as plt
from PIL import Image

with TemporaryDirectory() as tmp_dir:
    fig_output_path = Path(tmp_dir) / "fractopo_workflow_visualisation.jpg"
    fractopo_workflow_visualisation.main(output_path=fig_output_path)

    figure, ax = plt.subplots(1, 1, figsize=(9, 9))
    with Image.open(fig_output_path) as image:
        ax.imshow(image)
        ax.axis("off")